Mensuration Stuff

How Does He Do It?

How do I solve for nuclear structures? The equations can have any number of solutions. How do I figure out the particular equation to solve the model? I don't! I solve for the geometry of the nucleus by following empirical laws which govern the string geometry of the nucleus. After I have a solved geometric model in hand, then I mensurate (measure) the model and scale it, then I write the loop equation. To try and develop an equation for a nuclear model, then solve the geometry is pointless. You can't write an equation to describe the geometry of something you've never seen. The universe is a system of geometry. Geometry is governed by empirical laws. Mathematics is derived from geometry as a numerical approximation of a geometric situation. The universe is not an equation. You must fathom the geometry of a situation before you can write an equation to describe it.

The Metric System: Why didn't I use it?

Yes, I know I have sinned against the conventions of science, forgive me. Metric units simply were not convenient for building the models at reasonable sizes. I tried different scales, but I always came back to inches and half inch units because the physical construction with the available materials (18 & 22 gage solid wire) yielded the best results at these scales. Obviously a proton does not really have 51 inches of string in it, and all models will have to have their scales recalculated when more nuclear quantities are known. I suppose an explanation of the significance of 51 inches is in order. The first model I dimensioned was the proton (P1). It had two nuclear strings, one equatorial and one sinusoidal-equatorial that wrapped twice around the particle. I was using 18 gage solid wire, and the equatorial string was 15 inches. I needed to make sure I cut enough wire for the sinusoidal string, and since the snap points on the equatorial string were all five inches apart, I decided the sinusoidal would have six inches of string between snap points. That would make the sinusoidal string 36 inches long. (36" + 15" = 51") It didn't take long for the size of the models to get out of hand using 18 gage wire, so I started using 22 gage solid wire and cutting all my dimensions by half. At this point, the units used to scale the models are irrelevant, just so long as all models use the same scale. Feel free to convert the scale to any value convenient for the type of modeling you are doing. If you're building the models by hand, benefit from my experience and stick with the half-inch units. They are just about perfect for modeling with insulated 22 gage solid wire. If you want to make larger classroom demonstration models, go with insulated 18 gage solid wire and 1 inch units. All the measurements on the shell model pages can be used directly for these larger models.

Another technique I've been using recently has been working nicely, and that is to simply fashion a bunch of 10" or 12" structural loops and use them to build the core structure of the particle. If you're building the larger models, even with the half-inch units they are starting to get unmanageably large and floppy. By starting with structural loops of manageable dimensions, you can scale the model later on paper. (You're likely going to have to perform this step anyway if you're hunting for new solution sets.) You can always rescale the existing models via their given loop ratios while modeling.

Check My Work

I don't profess to be any brilliant math-head... I make lots of mistakes, that's how I learn. I wrote some computer routines to assist in mensuration of the models. I normally write code in QuickBASIC, but I found that QuickBASIC does not support the inverse sine function required for many of the calculations. I wound up writing the program on an old Texas Instruments "TI-74 BASICALC." It has proved indispensible to me. I have some diagrams which I used to make the calculations, they are basically two dimensional shadows of the poles of the particles. Rather than try and duplicate all of the solutions (which were solved by my TI-74), I'm providing the diagrams and several shortcuts to mensurating the models based on those calculations. If you have some spare time, check my shortcuts to make sure I didn't blow it. (If you just happen to have a TI-74 lying around, here are a couple of subroutines you can punch in to assist in the calculations. TI-74.TXT.)

Note: (20MAY97) I recently purchased Microsoft Excel 5.0 after taking a one day class on its use at work. I've never used a spreadsheet before, primarily because I didn't see the need, and they tend to be expensive, particularly if you don't know how to use one in the first place. Once I saw how easy it made things, I couldn't understand how I got along without it. I've created a quick little worksheet that will convert the scale of your models to whatever scale factor suits your needs (as long as they have no more than five loop values). I'm not sure how your browser will react to the worksheet link above. It may open Excel, it may want you to save it to disk, or it may not do anything. Netscape opens Excel on my local drive. (At the time of this writing, I still haven't contacted a host server for this site, so I'm not sure about a few HTML & FTP parameters.) I'm going to try and work up some spreadsheets to assist in mensuration of the models. Perhaps I'll be able to slap a few of them in place before my projected publication date. I'm shooting for 04JUL97, but I doubt I'll be finished with it by then.

Okay, here's a rather large worksheet containing most of the numerical data used to set up the shell pages. It's about a 400K file, rather large, and if you don't have a lot of memory in your computer, Excel may balk at it if you view it online. Chemists will definitely want to copy this spreadsheet to their local drive. Most fields are locked except scale and sinusoidal string values, but the sheets are not password protected. I recommend you make a backup copy of the original under a different filename before you start plugging in new values. The spreadsheets are copyrighted, by the way, and you can use them for personal use, but you may not publish the nuclear data contained in them or the spreadsheets themselves without permission of the copyright holder. That would be me.

nukelog2.xls

About Those Sinusoidal Strings...

I honestly do not know what will govern the amplitude of sinusoidal strings on most of the models which sport them, but I assumed their limits could be determined by constraints of the geometry. What I have done in the spreadsheet is to calculate them at what I suspect will be their maximum value in a cold shell. I went about this by taking the chord between two quarks on the equator and multiplying it by pi. This gives the circumference of a circle which would just touch both of the quarks. Multiply this circumference by half the number of snap points on the sinusoidal string to arrive at the length of the sinusoidal string. I think this is the upper limit because after providing enough string to create circlets with only two snap points on the nuclear shell, the potential for a violation of the laws governing the shell geometry starts to arise, possibly prompting a redistribution of the shells' energy. That is not a cold shell anymore. I suspect the sinusoidal strings will approach this value, and that which prevents them from forming into loops is that they follow the spherical curvature of the nuclear shell, to form circlets they would have to drop beneath the surface of the shell to lie on the chord. I do not know if they can do that or not. My gut feeling is no, but my guts have been wrong before. All of the models pictured have actually been created using shorter sinusoidal strings than the lengths given in the tables. The minimum length for a sinusoidal string will approach the length of an equatorial string for sinusoidals which go once around the shell, 2 x equatorial for sinusoidals which go twice around the shell. Its easier to model with wire near the upper limit than at the lower, though, so that is what I've given. Feel free to trim back the sinusoidal string lengths for modeling, I just guessed at their lengths when I created the models pictured on this web site. The angle of intersection on the quarks may be what sets the actual amplitude of the sine wave in nature, but that is very conjectural.

The following images are the actual calculations I performed to mensurate the P5 shells, including errors and corrections. Yeah, it's sloppy, but I wasn't concerned so much with pretty as with correct results. Much of the difficulty was in the mensuration of the filler circlets, there were a large number of steps involved in their calculation. Scroll on down the page for a much quicker and easier method of determining the circumference of a circumscribed triangle.

P5 Original Mensuration (3 Images)

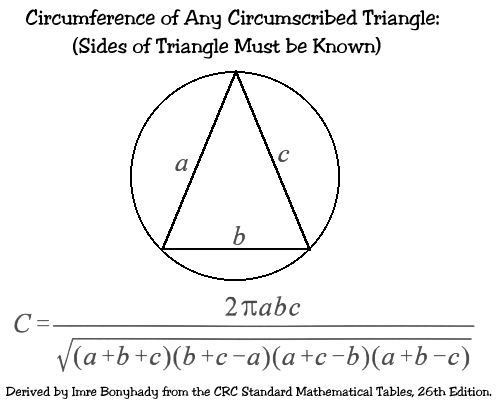
The slick little formula below was derived by Imre Bonyhady. I challenged an aquaintance at work, Mark Robb, to come up with a shortcut formula to do the filler circlet mensuration. He passed the challenge along to his friend, Imre Bonyhady. Imre was up to the challenge, and spent an evening of pencil work deriving this from the CRC Standard Mathematical Tables, 26th Edition. I knew there was a way to do it, but I couldn't find a formula and I already had my hands full doing multiple shell mensurations. I should point out that all the formulas and mensuration calculations are based on or derived from the CRC chapter on mensuration. It is a pleasent discovery for me to find that the math of nuclear geometry is not out of reach of anyone with a rudimentary knowlege of geometry, algebra, and trigonometry. I've read many physicists and mathematicians state the opinion that you must have advanced mathematics training to do anything useful in physics these days. I'm afraid I don't have any such training, but I think that nuclear geometry is probably going to turn out to be rather useful in spite of it.

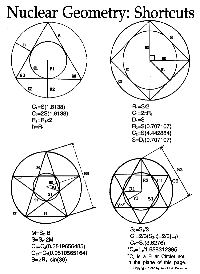
The shortcuts below are just a few useful relations to get things moving. There are several more. Keep in mind that these shortcuts are describing spherical objects, not flat two-dimensional images.

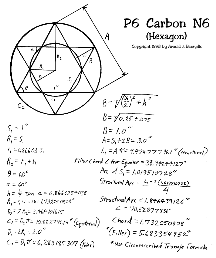
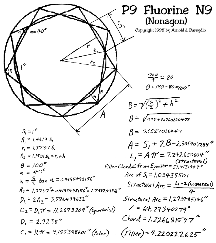
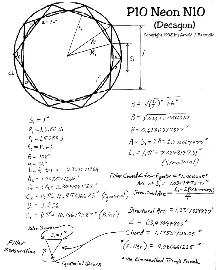
I re-calculated the models in a more consistent format, also prettier, but again, the calculations are frequently done on the TI-74. Click on the images below for a full-sized (readable) version. Oh, by the way, you can drop the last three decimal places off of these calculations, I tend to write out the entire mantissa of my TI-74 even though the accuracy of the calculations is limited to about four decimal places by the trig tables used.

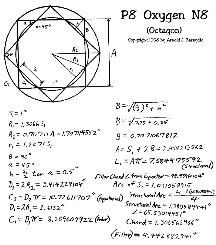
Home
Chemistry Notes
Key to Nuclear Models
Nuclear Shells
Empirical Laws
How to Build Them
Glossary